Уравнение Бернулли
Энергия в физике — это скалярная физическая величина, которая характеризует способность системы совершать работу. Она существует в разных формах и может переходить от одной формы в другую, но она никуда не может исчезнуть или возникнуть из ниоткуда (согласно закону сохранения).
Кинетическая — энергия, связанная с движением объекта. Так, движущаяся машина обладает кинетической энергией.
Потенциальная — энергия, связанная с положением объекта в поле сил — гравитационное или электростатическое поле. Объект, находящийся на высоте, имеет гравитационную потенциальную энергию.
Тепловая — энергия, связанная с хаотическим движением частиц внутри вещества, также называется внутренней.
Электрическая и магнитная — энергия, связанная с электрическими зарядами и магнитными полями.
Химическая — энергия, заключенная в химических связях между атомами и молекулами.
Ядерная — энергия, связанная с взаимодействиями внутри атомных ядер.
Кинетическая
Кинетическая — это энергия, которую имеет тело или система благодаря своему движению. Чем быстрее движется объект и чем больше его масса, тем больше у него кинетическая энергия.

Свойства кинетической энергии
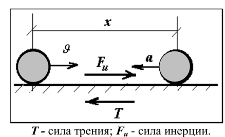
● Зависимость от скорости. Кинетическая энергия пропорциональна квадрату скорости. Это значит, что при увеличении скорости в два раза, кинетическая энергия увеличится в четыре раза.
● Суммарная кинетическая энергия. Если система состоит из нескольких тел, суммарная кинетическая равна сумме кинетических энергий всех тел в системе.
● Переход в другие формы. Кинетическая энергия может превращаться в другие виды. Так, при торможении автомобиля его кинетическая энергия преобразуется в тепловую тормозных колодок.
Кинетическая энергия является одной из важнейших концепций в физике и играет ключевую роль в понимании динамики объектов и систем.
Потенциальная
Потенциальная — это энергия, которую объект или система имеет благодаря своему положению в поле сил или состоянию. Она связана с возможностью совершить работу при изменении этого положения или состояния. Потенциальная энергия существует в нескольких формах, наиболее распространенными из которых являются гравитационная и упругая потенциальная.
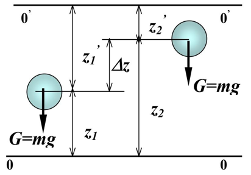
Гравитационная потенциальная
Гравитационная потенциальная энергия связана с положением объекта в гравитационном поле на Земле. Она определяется высотой объекта над определенным уровнем (обычно это уровень земли) и его массой.
Формула гравитационной потенциальной энергии

Упругая потенциальная
Упругая потенциальная энергия возникает в системах, которые могут быть растянуты или сжаты: в пружинах или эластичных материалах. Она накапливается в результате деформации, и система может совершить работу при возвращении в исходное состояние.

Общие свойства
●Зависимость от положения. Потенциальная энергия всегда связана с положением объекта или его конфигурацией относительно других объектов или полей сил.
● Относительность. Потенциальная энергия зависит от выбора точки отсчета. Высота объекта, а значит и его гравитационная потенциальная, зависит от того, какую точку выбрали за ноль.
● Преобразование в другие виды. Потенциальная энергия может переходить в другие формы, к примеру, в кинетическую. Когда объект падает, его гравитационная потенциальная энергия превращается в кинетическую.
●Закон сохранения. В изолированной системе сумма кинетической и потенциальной энергий остается постоянной, если отсутствуют потери на трение и другие неупругие процессы. Это является проявлением закона сохранения.
Потенциальная энергия играет важную роль в анализе динамики систем. Она позволяет описывать и прогнозировать движения объектов в различных полях сил, таких как гравитационное, электрическое и магнитное.
Что такое идеальная жидкость
Идеальная жидкость — это модель жидкости, которая обладает следующими идеализированными свойствами.
● В идеальной жидкости отсутствуют силы внутреннего трения (вязкости). Это означает, что слои могут двигаться относительно друг друга без сопротивления. На практике, в реальных веществах всегда присутствует вязкость, хотя в иногда ее можно считать пренебрежимо малой.
● Идеальная является несжимаемой, то есть ее плотность остается постоянной независимо от давления или других воздействий. В реальности вещества могут быть сжимаемыми, но для большинства практических задач сжимаемость воды и других так мала, что ее можно игнорировать.
● В идеальной жидкости отсутствует перенос тепла между частями, что упрощает описание ее поведения. Реальные субстанции могут проводить тепло, что приводит к сложным эффектам при их движении.
Применение модели идеальной жидкости
Модель идеальной жидкости используется для упрощения анализа движения жидкости в гидродинамике и аэродинамике.
● Уравнение Бернулли. Это фундаментальное уравнение для идеальной жидкости, которое связывает скорость, давление и высоту в потоке. Оно широко применяется в гидродинамике для описания потоков и работы гидравлических систем.
● Закон Паскаля. Для идеальной жидкости можно точно использовать закон Паскаля, который утверждает, что изменение давления в какой-либо части жидкости передается без изменений во все другие ее части.
Хотя модель идеальной жидкости полезна для теоретических расчетов и дает хорошее приближение во многих задачах, она не учитывает важные явления, такие как турбулентность, реальная вязкость и теплопроводность. Для более точного описания поведения реальных жидкостей используются более сложные модели, которые учитывают эти факторы.
Закон сохранения энергии идеальной жидкости
Закон сохранения энергии для идеальной жидкости выражается через уравнение Бернулли. Это уравнение связывает давление, скорость и высоту в движущейся идеальной несжимаемой жидкости, учитывая, что энергия в потоке сохраняется.
Уравнение для идеальной жидкости записывается в виде:

Оно показывает, что сумма трех членов — давления, кинетической энергии на единицу объема и потенциальной энергии на единицу объема — остается постоянной вдоль линии тока в идеальной жидкости. Если жидкость движется по трубе, у которой сечение меняется, то в узких местах скорость потока будет выше, а давление — ниже, чтобы сохранить постоянной сумму по уравнению. Уравнением бернулли для идеальной жидкости также объясняется принцип работы крыла самолета. Воздух движется быстрее над крылом, где создается область пониженного давления, что приводит к подъемной силе.
Уравнение применимо только для идеальной жидкости, т.е. несжимаемой, невязкой и без теплопроводности. В реальных жидкостях и газах вязкость, сжимаемость и турбулентность могут существенно влиять на поведение потока, и тогда необходимо использовать более сложные уравнения, такие как уравнения Навье-Стокса.
Реальная жидкость
Реальная жидкость обладает всеми реальными физическими свойствами, такими как вязкость, сжимаемость, теплопроводность и т.д., и поведение которой отличается от идеальной жидкости, принятой в упрощенных моделях.
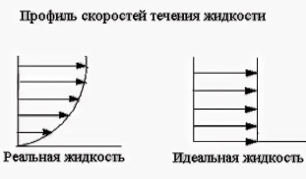
Основные характеристики реальной жидкости
● Вязкость. Вязкость вызывает диссипацию в потоке, что приводит к потерям давления и изменению скорости течения жидкости. Вязкость приводит к тому, что скорость потока жидкости вблизи стенок трубы меньше, чем в центре потока (профиль скорости параболический).
●Сжимаемость. В отличие от идеальных жидкостей, которые считаются несжимаемыми, реальные жидкости могут изменять объем под воздействием давления. Вода сжимаема, хотя и очень незначительно при нормальных условиях. Сжимаемость важна при рассмотрении потоков жидкостей при высоких давлениях, а также при звуковых волнах в жидкости.
● Турбулентность. В реальных жидкостях часто наблюдается турбулентный поток, особенно при высоких скоростях или в сложной геометрии. Турбулентность сопровождается хаотическими вихревыми движениями, которые усиливают диссипацию. Идеальная жидкость предполагает ламинарный поток, где все частицы жидкости движутся параллельно друг другу без перемешивания между слоями.
●Теплопроводность. Реальные жидкости могут передавать тепло через теплопроводность, что влияет на распределение температуры в жидкости и может изменять ее свойства, такие как вязкость.
●Наличие поверхностного натяжения. В реальных жидкостях существует поверхностное натяжение, которое влияет на поведение жидкости на границе с другими средами, при образовании капель или пузырьков.
Закон сохранения энергии для реальной жидкости
Закон сохранения энергии для реальной жидкости учитывает такие факторы, как вязкость и теплопроводность, которые отсутствуют в модели идеальной жидкости. Эти факторы вызывают потери, обычно проявляющиеся в виде тепла, а также в изменении давления и скорости жидкости.
Для реальной жидкости закон сохранения энергии можно записать в виде уравнения Бернулли, с учетом потерь на трение и других факторов.

Источники потерь
● Вязкость. Реальные жидкости имеют внутреннее трение (вязкость), которое приводит к преобразованию части механической жидкости в тепловую. Эти потери особенно заметны при движении жидкости через узкие трубы или при турбулентных потоках.
● Турбулентность. В реальных потоках жидкости часто возникает турбулентность, которая также приводит к потере. Турбулентные потоки характеризуются хаотическими вихрями и пульсациями, которые вызывают дополнительное трение и диссипацию.
● Теплопроводность. В реальных жидкостях могут происходить тепловые потоки между различными участками жидкости, что приводит к изменению температурного поля и перераспределению.
● Сжимаемость. При высоких скоростях потока или при значительных изменениях давления, может проявляться сжимаемость жидкости, что также влияет на сохранение.
В инженерной практике для расчета реальных систем, таких как трубопроводы, насосы, гидравлические системы, используют 2 уравнения Бернулли. Это делается с помощью специальных коэффициентов сопротивления, которые включаются в уравнения. Уравнение Дарси-Вейсбаха используется для расчета потерь давления в трубопроводах из-за трения. Формулы для расчета потерь на местных сопротивлениях учитывают потери при прохождении жидкости через сужения, повороты, клапаны и другие элементы трубопроводов.
Закон сохранения энергии для реальной жидкости учитывает необратимые процессы, такие как вязкость и турбулентность, что приводит к потере части механической энергии в виде тепла и других форм. Эти факторы делают анализ реальных жидкостей сложнее, чем для идеальных жидкостей, но они важны для точного понимания и прогнозирования поведения потоков в различных практических приложениях.
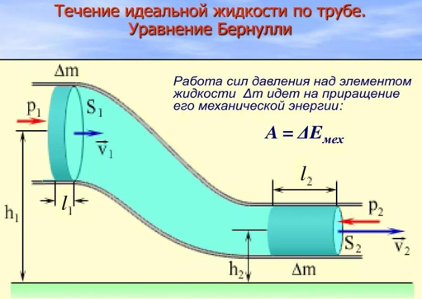
Уравнение Бернулли
Уравнением для потока жидкости называют фундаментальное уравнение в гидродинамике, которое описывает закон сохранения энергии для потока идеальной жидкости (некоторые с низкой вязкостью могут быть приближены к идеальным в этом контексте). Оно связывает члены уравнения Бернулли: скорость и высоту, показывая, что в движущейся сумма этих параметров остается постоянной вдоль линии тока.
Определение полному уравнению Бернулли дал швейцарский математик и физик Даниилом Бернулли в 1738 году. Оно возникло в результате работы Бернулли над законом сохранения энергии, а также исследований в области гидродинамики и аэродинамики.
История
Даниил Бернулли был членом знаменитой семьи Бернулли, которая внесла значительный вклад в развитие математики и физики. Труд Бернулли "Hydrodynamica" (1738 год) стал основополагающим для понимания движения жидкостей и газа. В этой книге он представил свое знаменитое уравнение, которое стало одним из первых выражений закона сохранения применительно к потокам жидкости.

Бернулли рассматривал поток несжимаемой идеальной жидкости и вывел уравнение, связывающее между собой давление, скорость и высоту жидкости на различных участках потока. Благодаря уравнению Бернулли для потока жидкости стало понятно, как давление изменяется в зависимости от скорости потока в различных частях трубы или канала.
В XVIII веке наука о движении жидкостей и газов находилась на стадии становления. Исследователи, такие как Исаак Ньютон и Эдм Марриотт, сделали значительные открытия, касающиеся законов движения, но многие аспекты поведения жидкостей оставались непонятными. Закон уравнения Бернулли помог объяснить многие наблюдаемые явления, такие как уменьшение давления в жидкости при увеличении скорости потока, что впоследствии стало основой для развития аэродинамики и гидравлики.
После публикации "Hydrodynamica" работа Бернулли не сразу получила широкое признание, но со временем его уравнение стало ключевым в гидродинамике. В XIX веке идеи Бернулли были развиты и уточнены другими учеными, такими как Леонард Эйлер, который помог формализовать и расширить применение уравнения Бернулли на более сложные задачи гидродинамики.
Вывод уравнения Бернулли до сих пор используется в различных инженерных дисциплинах, таких как аэродинамика, гидротехника, трубопроводные системы, проектирование самолетов и судов, а также в медицине, к примеру, для объяснения принципов работы сердца и кровеносных сосудов.
Таким образом, работа Бернулли не только является важным историческим достижением, но и продолжает играть ключевую роль в современной науке и технике.
Физический смысл уравнения Бернулли
Уравнение Бернулли выражает принцип сохранения энергии в идеальной несжимаемой жидкости, которая течет вдоль линии тока. Его физический смысл заключается в том, что в идеальном потоке жидкости сумма трех видов (кинетической, потенциальной из давления и потенциальной из высоты) остается постоянной.
Физический смысл основных компонентов уравнения Бернулли
● Давление
Удельная потенциальная энергия давления описывает способность жидкости производить работу за счет давления. Чем выше давление, тем больше потенциальная энергия жидкости.
● Кинетическая
Удельная кинетическая энергия жидкости, которая связана с движением жидкости. Чем выше скорость потока, тем больше кинетическая.
● Гравитационная потенциальная
Удельная потенциальная энергия, связанная с высотой точки относительно выбранного уровня отсчета. Чем выше точка в гравитационном поле, тем больше потенциальная.
Принцип работы уравнения
Уравнение демонстрирует, что в идеальной жидкости, когда нет потерь на трение и другие факторы, полная механическая энергия в любом сечении потока сохраняется. То есть, сумма давления, кинетической энергии и потенциальной энергии высоты постоянна вдоль линии тока.
Если скорость потока увеличивается, то чтобы сохранить постоянство энергии, давление должно уменьшаться. И наоборот, если скорость уменьшается, давление увеличивается. Это объясняет эффект воздушного потока над крылом самолета, где увеличение скорости потока над крылом приводит к понижению давления и созданию подъемной силы.

Уравнение используется для анализа потоков в трубопроводах, каналах, для проектирования систем водоснабжения, и в аэродинамике для расчета подъемной силы и сопротивления. Таким образом, формула представляет собой количественное выражение закона сохранения энергии в потоке жидкости и позволяет понять, как различные формы энергии взаимосвязаны в потоке.
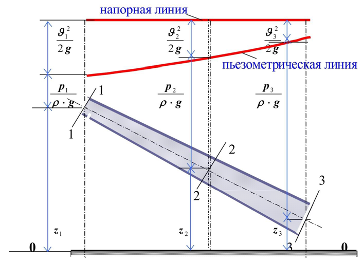
Диаграмма Бернулли
Диаграмма Бернулли — это графическое представление уравнения Бернулли, которое позволяет визуализировать изменения давления, скорости и высоты вдоль потока идеальной несжимаемой жидкости. Диаграмма Бернулли помогает понять, как различные виды энергии взаимодействуют и сохраняются в потоке.
Шаги для построения диаграммы Бернулли
- Определите параметры потока: скорость, давление, высоту, плотность (если известна, но обычно плотность жидкости является постоянной).
- Выберите сечения несколько точек вдоль линии тока, где будете измерять параметры потока: скорость, давление и высоту. Это могут быть точки на входе и выходе из трубы, через которую течет жидкость.
- Измерьте скорость, давление, и высоту в каждом выбранном сечении.
- Для каждой точки вычислите компоненты: удельная кинетическая энергия, удельная потенциальная энергия давления, удельная гравитационная потенциальная энергия.
- Постройте график Бернулли. На горизонтальной оси отложите параметры (позиции в трубе или точки потока). На вертикальной оси отложите значения удельных энергий.
- Нанесите данные на график Бернулли. Нанесите графики для каждой из трех компонент. Вы можете использовать разные цвета или линии для разных компонентов.
- Постройте итоговую диаграмму Бернулли. В итоге на диаграмме должна быть видна сумма всех трех компонент в разных точках потока. Для идеальной жидкости эта сумма должна оставаться постоянной вдоль линии тока, что подтверждает закон сохранения энергии.
Предположим, у вас есть труба с двумя сечениями.
- Воспользуйтесь уравнением Бернулли для сечений. Вычислите удельные энергии для каждой точки.
- Нанесите на график Бернулли соответствующие значения для давления, скорости и высоты.
- Проверьте, что сумма всех этих компонент остается постоянной.
Использование диаграммы Бернулли
Диаграмма Бернулли помогает визуализировать и проанализировать распределение энергии в потоке жидкости. Диаграмма Бернулли полезна для:
- Оценки потерь давления.
- Определения изменений скорости и высоты в различных точках.
- Проектирования и анализа гидравлических и аэродинамических систем.
Для реальной жидкости диаграмма Бернулли немного усложняется из-за потерь энергии, связанных с вязкостью, турбулентностью и другими факторами, которые не учитываются в идеальной модели. Однако диаграмму можно адаптировать, чтобы учесть эти потери.
Шаги для построения диаграммы Бернулли для реальной жидкости
- Определите параметры потока: скорость, давление, высота, плотность.
- Измерьте параметры. Как и в идеальном случае, измерьте скорость, давление и высоту в выбранных точках потока.
- Определите потери давления, вызванные трением и турбулентностью, которые могут быть вычислены или оценены с помощью коэффициентов сопротивления, таких как потери на местных сопротивлениях.
- Адаптируйте уравнение. Для реальной жидкости оно модифицируется для учета потерь энергии.
- Постройте диаграмму Бернулли. На горизонтальной оси отложите параметры потока (различные точки вдоль трубопровода). На вертикальной оси отложите значения удельных энергий.
- Нанесите значения Бернулли. Включите все компоненты для каждой точки и укажите потери давления.
На диаграмме Бернулли видно, как различные компоненты энергии изменяются между точками потока. Потери энергии будут видны в виде дополнительных «провалов» или корректировок в значениях давления и энергии.
Диаграмма Бернулли для реальной жидкости позволяет визуализировать, как реальные потери энергии влияют на параметры потока и помогает в оценке эффективности систем и проектировании.
Суммарные потери напора
Суммарные потери напора — это суммарное снижение давления, которое происходит в потоке жидкости из-за различных факторов, таких как трение, турбулентность и другие диссипативные эффекты. Эти потери нельзя учесть в идеальном уравнении Бернулли, которое предполагает отсутствие потерь. В реальных системах эти потери учитываются для точной оценки поведения потока.
Основные источники потерь напора
● Потери на трение
Возникают из-за вязкости жидкости и трения о стенки трубопровода. Эти потери можно оценить с помощью уравнения Дарси-Вейсбаха.

● Потери на местные сопротивления
Возникают из-за изменений в геометрии потока, таких как повороты, расширения и сужения. Эти потери вычисляются с использованием локальных коэффициентов сопротивления.
● Потери на завихрения и турбулентность
Эти потери сложно оценить точно, так как зависят от сложности потока и его режима. Обычно учитываются в виде потерь на трение и местные сопротивления.
● Суммарные потери напора
Суммарные потери напора представляют собой сумму всех потерь в системе.
При использовании уравнения Бернулли для реальных жидкостей суммарные потери напора учитываются как дополнительный член.
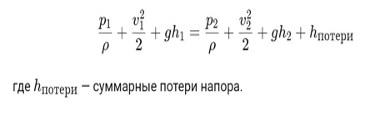
Эти потери необходимо учитывать при проектировании и анализе систем водоснабжения, трубопроводов и других гидравлических систем для обеспечения их эффективной работы.
Местные потери напора
Местные потери напора — это потери давления, возникающие в потоке жидкости из-за изменений в геометрии трубопровода, таких как изгибы, расширения, сужения и другие конструкции, которые нарушают равномерное движение жидкости. Эти потери отличаются от потерь на трение, которые возникают из-за трения жидкости о стенки трубы по всей длине трубы.
Определение местных потерь напора
Местные потери напора зависят от типа конструкции и характеристик потока. Они могут быть выражены через локальный коэффициент сопротивления и скорость потока. Формула для расчета местных потерь напора имеет вид:

Коэффициенты сопротивления
Коэффициенты сопротивления (K) зависят от конструкции и могут быть найдены в справочниках или определены экспериментально.
● Повороты
Поворот трубы под углом 90°: K может варьироваться от 0,5 до 1,5 в зависимости от радиуса кривизны и типа поворота.
● Расширения и сужения
Переходное расширение или сужение: K обычно находится в диапазоне от 0,5 до 2,0.
● Арматура и клапаны
Клапаны, задвижки и арматура могут иметь K в диапазоне от 1,0 до 10,0 в зависимости от типа и состояния.
Местные потери напора часто учитываются при проектировании и анализе трубопроводных систем, вентиляционных систем и водоснабжения. Они помогают определить общее падение давления в системе, что критично для обеспечения эффективной работы насосов, вентиляторов и других устройств.
Знание и правильный расчет местных потерь напора позволяют избежать избыточного расхода энергии и поддерживать нужный уровень давления на различных участках системы.
Выводы уравнения Бернулли
● Обратная зависимость между скоростью и давлением. При увеличении скорости потока жидкости давление понижается, и наоборот. Это объясняет эффект работы крыла самолета, где над крылом воздух движется быстрее, создавая область пониженного давления и подъемную силу.
● Сохранение полной механической энергии. Вдоль линии тока для идеальной несжимаемой жидкости сумма удельной кинетической энергии, удельной потенциальной энергии давления и удельной потенциальной энергии высоты остается постоянной.
● Взаимодействие давления и высоты. При увеличении высоты жидкости (при подъеме по трубе) давление уменьшается, если скорость потока остается неизменной.
● Постоянство вдоль линии тока. Уравнение применимо вдоль линии тока; в разных точках одного и того же потока могут быть разные скорости, давления и высоты, но их комбинация остается постоянной.
Применение уравнения Бернулли
Применение уравнения в гидротехнике особенно важно для расчета потоков воды, проектирования гидротехнических сооружений и систем водоснабжения. В этой области уравнение помогает анализировать движение воды через различные конструкции, оценивать напор, давление, скорость потока и потери.
● Проектирование трубопроводов и каналов
В водопроводных и канализационных системах оно используется для оценки распределения давления вдоль труб и каналов. В идеальной системе (без потерь на трение) уравнение помогает рассчитать, как меняются давление и скорость воды при движении по трубе. В реальных системах добавляются поправки на трение и местные сопротивления, такие как сужения или изгибы труб. Расчет позволяет определить скорость воды в разных участках трубопровода, особенно при изменении сечения трубы или высоты.
● Гидроэлектростанции
С помощью уравнения Бернулли для напора жидкости можно рассчитать напор воды, который создается при ее падении с высоты. Напор — это потенциальная, которая преобразуется в кинетическую энергию, приводящую в движение турбину. С помощью уравнения энергии и уравнения Бернулли можно оценить эффективность преобразования воды в электроэнергию, учитывая потери на трение и турбулентность.
● Дамбы и водохранилища
Контроль за уровнем воды. Благодаря уравнению Бернулли можно оценить течение жидкости и провести анализ водотоков через водосбросы и шлюзы дамб. Оно позволяет определить, с какой скоростью вода будет вытекать через водосброс при различных уровнях воды в водохранилище. Важной задачей является управление объемом воды, который проходит через дамбу. Формула помогает точно рассчитать объем и скорость потока, чтобы предотвратить перелив воды или разрушение конструкции.
● Гидравлические насосы и турбины
Используется для расчета характеристик насосов, таких как подача и напор. Оно помогает определить, какое давление и скорость нужно создать для эффективного перекачивания воды. Для расчета работы гидравлических турбин, которые преобразуют кинетическую и потенциальную силу воды в механическую работу, расчет помогает определить оптимальные условия потока.
● Регулирование потока
В плотинах и водосбросах оно используется для анализа потоков воды через регулируемые затворы. Это позволяет управлять потоком воды в зависимости от уровня в водохранилище и потребностей в водообеспечении или энергетике. При проектировании плотин и водосбросов помогает оценивать риск перелива воды и расчеты для предотвращения наводнений, учитывая скорость и давление потока при разных уровнях воды.
● Применение закона Вентури
Уравнение используется для проектирования трубопроводов с сужениями (эффект Вентури). В местах сужения трубы скорость воды увеличивается, а давление падает, что может использоваться для контроля потока или измерения расхода воды. Также расходомеры основаны на уравнении Бернулли и используются для измерения расхода воды в трубопроводах путем измерения разницы давления до и после сужения.
● Гидравлические прыжки
В каналах и реках часто используются гидравлические прыжки для уменьшения скорости потока и предотвращения эрозии берегов. С помощью уравнения Бернулли для струйки жидкости можно рассчитать параметры этих прыжков, такие как высота и длина, чтобы эффективно регулировать поток.
Предположим, что вода течет по трубе, соединяющей водохранилище и турбину. В начальной точке трубы вода имеет определенную потенциальную Е из-за высоты водохранилища. По мере того, как вода спускается по трубе, ее потенциальная Е преобразуется в кинетическую, что увеличивает скорость потока. Уравнение можно использовать для расчета скорости воды перед входом в турбину, что позволяет оценить количество Е, которую можно получить.
● Медицинская техника
В медицине оно используется для измерения скорости кровотока через сосуды с помощью допплеровских ультразвуковых приборов. Различия в скорости крови в разных участках сосуда позволяют оценить изменения в давлении, что важно для диагностики заболеваний, таких как стеноз артерий. Также применяется в анализе и проектировании дыхательных аппаратов, чтобы понять, как изменяется давление воздуха в легких во время вдоха и выдоха.
● Гидравлические и пневматические устройства
В двигателях внутреннего сгорания и других механизмах, где происходит смешивание топлива и воздуха, уравнение помогает рассчитать необходимые параметры для оптимального функционирования устройства. Для определения мощности и работы гидротурбин и мельниц оно используется для анализа потоков воды, поступающих на лопатки.
● Химическая промышленность
В химических реакторах и абсорбционных колоннах, где важны точные параметры потоков газа и жидкости, расчет помогает оптимизировать процессы. Уравнение является важным инструментом в физике и инженерии, поскольку позволяет прогнозировать и контролировать поведение жидкостей и газов в различных системах и устройствах.
● Аэродинамика
Уравнение также объясняет принцип полета самолета. Оно используется для анализа подъемной силы, создаваемой на крыльях самолета, где разные скорости потока воздуха над и под крылом приводят к разнице в давлении и, следовательно, к подъемной силе. В вентиляционных системах и системах кондиционирования воздуха уравнение помогает рассчитать распределение давления и скорости воздуха по системе.
Это мощный инструмент в гидротехнике, который позволяет инженерам проектировать и оптимизировать системы водоснабжения, гидроэлектростанции, дамбы и другие гидротехнические сооружения. Оно помогает прогнозировать поведение потока воды в различных условиях, что необходимо для обеспечения безопасности и эффективности работы этих систем.
